Gradients of GAN Objectives
This technical post will offer a new view of common training objectives for generative adversarial networks (GANs), including a justification for the widely-used non-saturating loss.
The gradient of the discriminator
First, let’s look at the original GAN loss function and show that it’s simpler than it looks. As defined in Goodfellow et al. (2014), it’s
![L(G, D) = \mathbb{E}_{x \sim p_\text{data}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]](/math/a031358542.png)
where 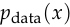 is the data distribution,
is the data distribution, 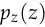 is the noise distribution,
is the noise distribution, 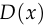 is the discriminator, and
is the discriminator, and 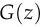 is the generator.
is the generator.
To analyze this loss function, we’ll use the same idea as in my post on the cross entropy loss: instead of looking at the function itself, we’ll look at its gradient.
We’ll assume the discriminator uses the standard method of obtaining the output probability 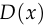 by applying the logistic sigmoid function to a scalar output
by applying the logistic sigmoid function to a scalar output 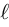 :
:
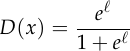
Taking the logarithm:
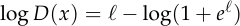
And the derivative:
![\begin{align*} \frac{\text{d}}{\text{d}\ell}[\log D(x)] &= \frac{\text{d}}{\text{d}\ell}[\ell - \log(1 + e^\ell)] \\ &= 1 - \frac{e^\ell}{1 + e^\ell} \\ &= 1 - D(x) \end{align*}](/math/04d1c57a5f.png)
This is quite surprising: by taking the derivative of 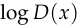 with respect to
with respect to 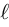 ,
, ,
,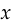 is fake.
is fake.
We can do the same calculation for the flipped probability 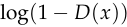 :
:
![\begin{align*} \frac{\text{d}}{\text{d}\ell}[\log(1 - D(x))] &= \frac{\text{d}}{\text{d}\ell}\left[\log\left(\frac{1}{1+e^\ell}\right)\right] \\ &= \frac{\text{d}}{\text{d}\ell}[-\log(1 + e^\ell)] \\ &= -\frac{e^\ell}{1 + e^\ell} \\ &= -D(x) \end{align*}](/math/047221b500.png)
We’re going to use these facts to analyze the discriminator loss function 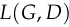 .
.
First, some change of notation: let’s write 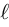 as
as 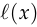 to make it clear what input produced
to make it clear what input produced 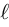 .
.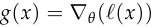 ,
,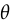 represents the parameters of the discriminator. The motivation for this definition of
represents the parameters of the discriminator. The motivation for this definition of 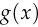 is that it will let us write the full gradient
is that it will let us write the full gradient ![\nabla_\theta[f(D(x))]](/math/fcdcc05473.png) as the product
as the product ![g(x) \cdot \frac{\text{d}}{\text{d}\ell}[f(D(x))]](/math/f3ec24f67d.png) ,
,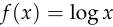 or
or 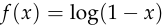 .
.
Now we can write the gradient of 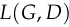 as follows:
as follows:
![\begin{align*} &\nabla_\theta \, L(G, D) \\ &= \nabla_\theta\left[ \mathbb{E}_{x \sim p_\text{data}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))] \right] \\ &= \mathbb{E}_{x \sim p_\text{data}(x)}[\nabla_\theta \log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\nabla_\theta \log(1 - D(G(z)))] \\ &= \mathbb{E}_{x \sim p_\text{data}(x)}[g(x) \cdot (1 - D(x))] + \mathbb{E}_{z \sim p_z(z)}[g(G(z)) \cdot (-D(G(z))) ] \\ &= \mathbb{E}_{x \sim p_\text{data}(x)}[g(x) \cdot (1 - D(x))] - \mathbb{E}_{z \sim p_z(z)}[g(G(z)) \cdot D(G(z)) ] \\ &= \hspace{1.05em} \mathbb{E}_{x \sim p_\text{data}(x)}[g(x) \cdot \text{Pr}(x\text{ is misclassified})] \\ &\hspace{1.2em} - \mathbb{E}_{z \sim p_z(z)}[g(G(z)) \cdot \text{Pr}(G(z)\text{ is misclassified}) ] \hspace{3em} (*) \end{align*}](/math/702e3da711.png)
This gives a clearer view of the GAN objective than looking at the original loss function. From this, we see that the discriminator’s goal is simply to increase 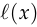 for real inputs and decrease
for real inputs and decrease 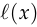 for fake inputs, with the caveat that inputs are weighted by their probability of being misclassified.
for fake inputs, with the caveat that inputs are weighted by their probability of being misclassified.
This is an example of a general principle in machine learning, which is that learning algorithms should focus on examples the model gets wrong over examples the model gets right. Other examples of this principle include:
- The perceptron learning algorithm, which only updates on mistakes.
- The hinge loss, which has no gradient when the prediction
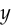 has the right sign and
has the right sign and 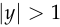 .
. - Logistic regression, which has the same loss function as a GAN discriminator.
The non-saturating loss
If we accept the principle that a model should weight its mistakes more than its successes, then there’s something not quite right about 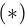 .
.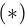 matches this principle when used for the discriminator, it’s quite the opposite for the generator. From the perspective of the generator, the examples which are misclassified by the discriminator are successes, not mistakes. Applying this principle to the training of the generator would suggest that we should weight more heavily the examples which are correctly classified by the discriminator. In fact, this is exactly what is done in practice. From Goodfellow et al. (2014):
matches this principle when used for the discriminator, it’s quite the opposite for the generator. From the perspective of the generator, the examples which are misclassified by the discriminator are successes, not mistakes. Applying this principle to the training of the generator would suggest that we should weight more heavily the examples which are correctly classified by the discriminator. In fact, this is exactly what is done in practice. From Goodfellow et al. (2014):
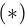 is the gradient of] may not provide sufficient gradient for
is the gradient of] may not provide sufficient gradient for  to learn well. Early in training, when
to learn well. Early in training, when  is poor,
is poor, 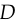 can reject samples with high confidence because they are clearly different from the training data. In this case,
can reject samples with high confidence because they are clearly different from the training data. In this case, 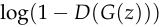 saturates. Rather than training
saturates. Rather than training 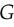 to minimize
to minimize 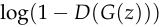 we can train
we can train 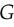 to maximize
to maximize 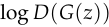 .
.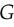 and
and 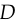 but provides much stronger gradients early in learning.
but provides much stronger gradients early in learning.
Though Goodfellow et al. motivate it differently, referring to vanishing gradients early in training, the idea is precisely the same: maximizing 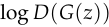 leads to weighting
leads to weighting 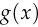 by the probability that
by the probability that 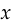 is correctly classified by the discriminator. This is called the non-saturating loss and it is used ubiquitously, for example in StyleGAN 2 (Karras et al., 2020).
is correctly classified by the discriminator. This is called the non-saturating loss and it is used ubiquitously, for example in StyleGAN 2 (Karras et al., 2020).
The hinge loss
The hinge loss has a long history, but its use in GANs dates to Lim and Ye (2017) and Tran et al. (2017). It was used in SAGAN (Zhang et al., 2018) and BigGAN (Brock et al., 2018).
Like the non-saturating loss, it uses different loss functions for the generator and the discriminator:
![\begin{align*} L_D &= -\mathbb{E}_{x \sim p_\text{data}(x)}[\min(0, -1 + D(x))] - \mathbb{E}_{z \sim p_z(z)}[\min(0, -1 - D(G(z)))] \\ L_G &= -\mathbb{E}_{z \sim p_z(z)}[D(G(z))] \end{align*}](/math/6905152cc6.png)
The gradient of this loss is similar to the gradient in 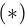 .
.![g(x) = \nabla_\theta[D(x)]](/math/808094d4b9.png) ,
,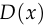 here is the analogue of
here is the analogue of 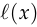 previously. The gradient of the discriminator is:
previously. The gradient of the discriminator is:
![\begin{align*} -\nabla_\theta \, L_D &= \hspace{1.05em} \mathbb{E}_{x \sim p_\text{data}(x)} \left[ \begin{cases} g(x) & \text{if $D(x) < 1$} \\ 0 &\text{otherwise} \end{cases}\right] \\ &\hspace{1.2em} - \mathbb{E}_{z \sim p_z(z)}\left[ \begin{cases} g(G(z)) &\text{if $D(G(z)) > -1$} \\ 0 &\text{otherwise} \end{cases} \right] \end{align*}](/math/d8a15a6888.png)
You can see the similarity to 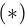 :
: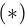 :
:
You can also see why it’s necessary to use a different loss function for the generator. Otherwise, the generator would get no gradient from examples the discriminator confidently classifies as fake, which is precisely the opposite of what we want.
You might ask whether the reasoning from the previous section on the non-saturating loss can also be applied here. In fact, there is a direct analogue of the non-saturating loss:
![L_G = -\mathbb{E}_{z \sim p_z(z)}[\min(0, -1 + D(G(z)))]](/math/ad13d7ab3b.png)
This cuts off the gradient using the same rule as 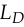 ,
,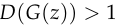 rather than when
rather than when 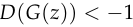 .
.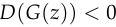 .
.
I’m not aware of anyone using this alternate loss. If you’ve tried it, let me know.
Adding a W
Now let’s consider the Wasserstein GAN (Arjovsky et al., 2017). WGAN can be obtained from the original GAN by making the following modifications:
- Stop weighting
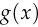 by the probability of
by the probability of 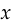 being misclassified. Instead, weight all
being misclassified. Instead, weight all 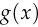 equally.
equally. - Enforce a Lipschitz constraint on
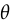 .
.
In the original paper, WGAN is presented differently. Arjovsky et al. motivate it by arguing that we should minimize the Wasserstein distance between the data distribution and the generator distribution, then proposing to use an alternative representation of the Wasserstein distance to approximate it using the discriminator. However, I prefer this presentation because it makes it clear that WGAN is very similar to the original GAN.
Why is my formulation of WGAN equivalent to that of Arjovsky et al.? Their formulation is to learn a discriminator 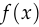 .
.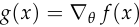 ,
,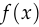 is the analogue of
is the analogue of 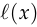 previously. The objective for their discriminator is to maximize
previously. The objective for their discriminator is to maximize
![\mathbb{E}_{x \sim p_\text{data}(x)}[f(x)] - \mathbb{E}_{z \sim p_z(z)}[f(G(z))]](/math/c3e2fa5396.png)
and the gradient of this quantity is
![\mathbb{E}_{x \sim p_\text{data}(x)}[g(x)] - \mathbb{E}_{z \sim p_z(z)}[g(G(z))]](/math/eaa7887e92.png)
which is equal to 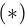 without the weighting by misclassification probability.
without the weighting by misclassification probability.
Why does WGAN add the Lipschitz constraint? This was motivated in the WGAN paper by the fact that a Lipschitz constraint is necessary to estimate the Wasserstein distance — specifically, if the Wasserstein distance between 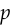 and
and 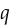 is
is 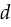 ,
,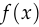 between
between 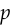 and
and 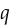 constrained to have Lipschitz constant
constrained to have Lipschitz constant 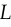 will satisfy:
will satisfy: ![\mathbb{E}_{x \sim p(x)}[f(x)] - \mathbb{E}_{x \sim q(x)}[f(x)] = L \cdot d.](/math/38cca38c6b.png)
But there’s another way to look at the Lipschitz constraint: we can view it as a regularizer on the discriminator that keeps its gradients bounded and makes the generator easier to optimize. This view is supported by Kurach et al. (2019), which found that spectral normalization, a common way of enforcing the Lipschitz constraint (Miyato et al., 2018), helped all GAN variants in their study, not just WGAN:
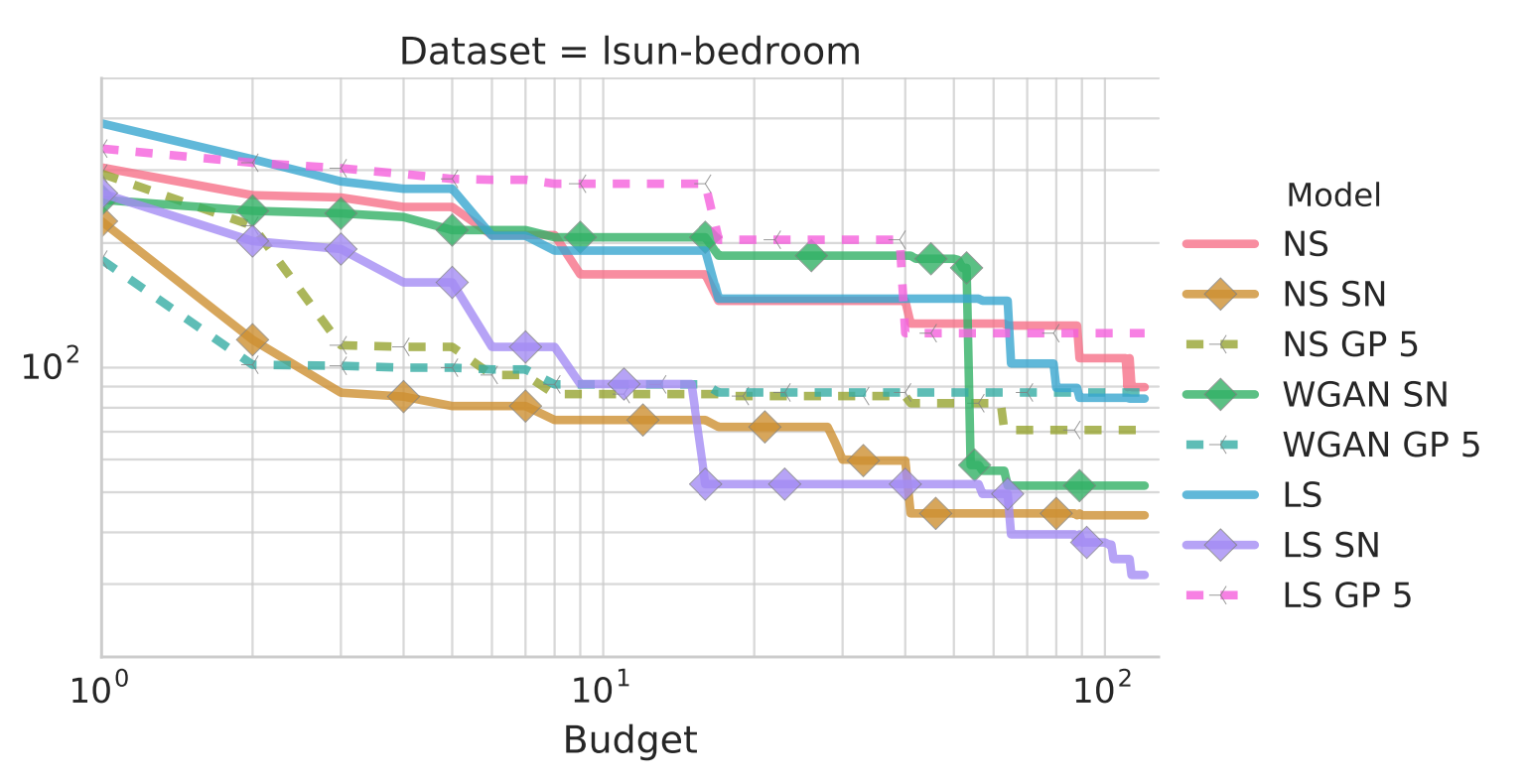
Subplot of Figure 2 from Kurach et al. (2019). NS means non-saturating loss, LS means least-squares loss, SN means spectral normalization, GP means gradient penalty (another way of enforcing the Lipschitz constraint). y-axis is FID.
Hopefully this post has given you a new way to think about GAN objectives. If you liked it, you might also like this other post, which applies the same idea to the cross entropy loss.





