A Justification of the Cross Entropy Loss

Aug 8, 2020

A wise man once told me that inexperienced engineers tend to undervalue simplicity. Since I’m not wise myself, I don’t know whether this is true, but the ideas which show up in many different contexts do seem to be very simple. This post is about two of the most widely used ideas in deep learning, the mean squared error loss and the cross entropy loss, and how in a certain sense they’re the simplest possible approaches.

Let’s start with the mean squared error, which is used when you want to predict a continuous value. If the model’s prediction was 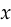$x$ and the correct answer was $y$ , then the mean squared error is defined as:

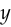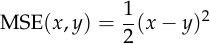
$\text{MSE}(x, y) = \frac{1}{2} (x - y)^2$

We can observe some basic facts about the mean squared error. It’s differentiable, so we can find its derivative with respect to 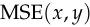$x$ , which lets us optimize the model parameters to minimize $\text{MSE}(x, y)$ using backpropagation. And it’s zero if and only if $x = y$ , so a model which successfully minimizes it has learned to produce the correct answer.

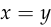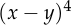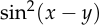
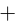
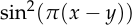But these facts don’t fully explain why people use mean squared error, since there are many other functions which also satisfy both properties. For example, $(x - y)^4$ and $\sin^2(x-y)$ $+$ $\sin^2(\pi(x-y))$ .

Instead, we should look at the derivative, which is beautifully simple:

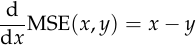
$\frac{\text{d}}{\text{d}x} \text{MSE}(x, y) = x - y$

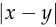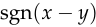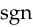Neither of the alternative functions mentioned above has such a simple derivative. The only function that comes close is $|x-y|$ , whose derivative is $\text{sgn}(x-y)$ , but most people would agree that a linear function is simpler than $\text{sgn}$ , which is nonlinear.

So, in plain English, the mean squared error is the loss function you get if you decide that your error signal should be equal to the difference between the output you wanted and the output your model gave. This explains why we should use it: why use anything more complicated if it’s not necessary?

The cross entropy

It turns out that a very similar argument can be used to justify the cross entropy loss. I tried to search for this argument and couldn’t find it anywhere, although it’s straightforward enough that it’s unlikely to be original.

The cross entropy is used when you want to predict a discrete value. To define it, we’ll need to change our framework to make the model output a probability distribution 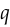$q$ instead of a scalar. The desired output will also be a distribution 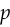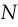$p$ . We’ll represent our probability distributions as non-negative vectors of $N$ elements which add to 1.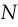 ( $N$ is the number of distinct values that our prediction target can take.)

The cross entropy is defined as:

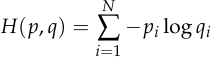
$H(p, q) = \sum_{i=1}^N -p_i \log q_i$

Just like the mean squared error, the cross entropy is differentiable, and it’s minimized if and only if 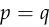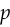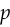$p = q$ . It’s also linear in $p$ , which lets us use the following trick to estimate its gradient using only a sample from $p$ instead of 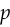$p$ itself (where 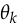$\theta_k$ is a model parameter):

$\begin{align*} \frac{\partial }{\partial \theta_k} H(p, q) &= \frac{\partial }{\partial \theta_k} \mathbb{E}_{i \sim p} [-\log q_i] \\ &= \mathbb{E}_{i \sim p} \left[\frac{\partial }{\partial \theta_k} (-\log q_i) \right] \end{align*}$

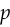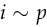This is essential for practical use because you don’t typically know the true distribution of labels ( $p$ ). Instead, you have a single label representing a sample from that distribution ( $i\sim p$ ), and you need to use it to estimate the gradient.

But even with the new constraint that the loss function should be linear in 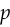$p$ , there are still many alternative functions which satisfy all these properties. In fact, Wikipedia has a list of them.

So what sets cross entropy apart? To answer this question, let’s make an additional assumption about our model: we assume it produces logits 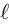$\ell$ and that its prediction 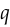$q$ is obtained from 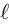$\ell$ using the softmax function:

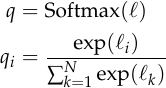
$\begin{align*} q &= \text{Softmax}(\ell) \\ q_i &= \frac{\exp (\ell_i)}{\sum_{k=1}^N \exp (\ell_k)} \end{align*}$

Expressed in terms of 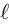$\ell$ , the cross entropy is:

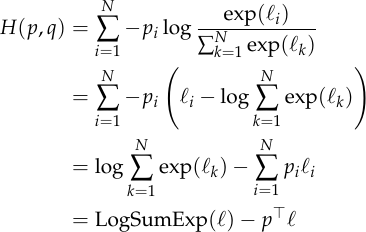
$\begin{align*} H(p, q) &= \sum_{i=1}^N -p_i \log \frac{\exp(\ell_i)}{\sum_{k=1}^N \exp(\ell_k)} \\ &= \sum_{i=1}^N -p_i \left(\ell_i - \log \sum_{k=1}^N \exp (\ell_k) \right) \\ &= \log\sum_{k=1}^N \exp(\ell_k) - \sum_{i=1}^N p_i \ell_i \\ &= \text{LogSumExp}(\ell) - p^\top \ell \end{align*}$

We can now take the gradient with respect to 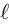$\ell$ . The gradient of LogSumExp is Softmax, which I like to remember with this diagram:

$Diagram illustrating that argmax is to max as Softmax is to LogSumExp (related by continuous relaxation)$

So the gradient of 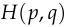$H(p, q)$ with respect to 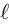$\ell$ is:

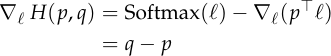
$\begin{align*} \nabla_\ell \, H(p, q) &= \text{Softmax}(\ell) - \nabla_\ell (p^\top \ell) \\ &= q - p \end{align*}$

This shows that the cross entropy is just like the mean squared error: its gradient is the difference between the output your model gives 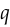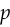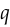( $q$ ) and the output you want ( $p$ ), provided that you look at its gradient with respect to the logits rather than $q$ itself. In this sense, cross entropy is the simplest loss function for classification, just as mean squared error is the simplest for regression.

See other posts